Öğrencinin T Dağılımını Hesaplamak İçin Formül
T dağılımını hesaplama formülü (popüler olarak Student's T Dağılımı olarak da bilinir), popülasyon ortalamasının (ikinci örneğin ortalaması) örnek ortalamasından (ilk örneğin ortalaması) yani (x̄ - μ) çıkarılması olarak gösterilir. başlangıçta o örnekteki birimlerin sayısı olan n'nin kareköküne bölünen ortalamaların standart sapmasına bölünür (s ÷ √ (n)).
T dağılımı, neredeyse normal dağılım eğrisine veya çan eğrisine benzeyen, ancak biraz daha şişman ve daha kısa kuyruklu bir dağılım türüdür. Örneklem büyüklüğü küçük olduğunda normal dağılım yerine bu dağılım kullanılacaktır.
t = (x̄ - μ) / (s / √n)
Nerede,
- x̄ örnek ortalamadır
- μ popülasyon ortalamasıdır
- s standart sapmadır
- n, verilen örneğin boyutu
T Dağılımının Hesaplanması
Student t dağılımının hesaplanması oldukça basittir, ancak evet, değerler gereklidir. Örneğin, nüfus ortalamasından başka bir şey olmayan evren anlamına gelen popülasyon ortalamasına ihtiyaç duyulurken, popülasyonun gerçekliğini test etmek için örneklem ortalamasının, popülasyon temelinde iddia edilen ifadenin gerçekten doğru olup olmadığı anlamına gelir ve Alınan herhangi bir örnek aynı ifadeyi temsil edecektir. Bu nedenle, buradaki t dağılım formülü, örnek ortalamayı popülasyon ortalamasından çıkarır ve ardından bunu standart sapmaya böler ve değeri standartlaştırmak için örneklem büyüklüğünün karekökü ile çarpılır.
Bununla birlikte, t dağılımı hesaplaması için aralık olmadığından, değer tuhaf gidebilir ve öğrencinin t dağılımının bir değere ulaşma sınırlamaları olduğu için olasılığı hesaplayamayız ve bu nedenle yalnızca daha küçük örneklem büyüklüğü için yararlıdır. . Ayrıca, bir puana ulaştıktan sonra olasılığı hesaplamak için, öğrencinin t dağılım tablosundan bunun değerini bulmak gerekir.
Örnekler
Örnek 1
Aşağıdaki değişkenlerin size verildiğini düşünün:
- Nüfus ortalama = 310
- Standart sapma = 50
- Örneklem boyutu = 16
- Örnek ortalama = 290
T dağılım değerini hesaplayın.
Çözüm:
T dağılımının hesaplanması için aşağıdaki verileri kullanın.

Dolayısıyla, T dağılımının hesaplanması şu şekilde yapılabilir:
Burada tüm değerler verilmiştir. Sadece değerleri birleştirmemiz gerekiyor.
T dağılım formülünü kullanabiliriz

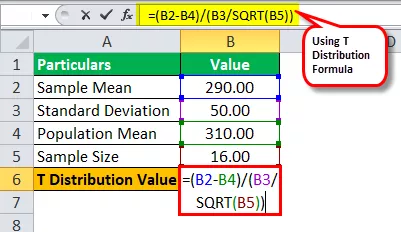
T = (290 - 310) / (50 / √16) değeri

T Değeri = -1.60
Örnek 2
SRH şirketi, analist seviyesindeki çalışanlarının saatte ortalama 500 $ kazandığını iddia ediyor. Analist düzeyinde 30 çalışandan oluşan bir örneklem seçildi ve saatlik ortalama kazançları 30 $ 'lık bir örnek sapmayla 450 $' dı. Ve iddialarının doğru olduğunu varsayarak, t dağılımının olasılığını bulmak için kullanılacak t dağılım değerini hesaplayın.
Çözüm:
T dağılımının hesaplanması için aşağıdaki verileri kullanın.
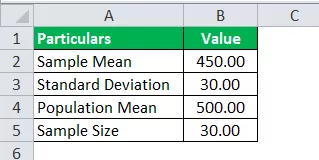
Dolayısıyla, T dağılımının hesaplanması şu şekilde yapılabilir:
Burada tüm değerler verilmiştir; sadece değerleri birleştirmemiz gerekiyor.
T dağılım formülünü kullanabiliriz


T = (450 - 500) / (30 / √30) değeri

T Değeri = -9,13
Dolayısıyla t skorunun değeri -9.13'tür.
Örnek 3
Universal College Board, rastgele seçilmiş 50 profesöre bir IQ seviyesi testi uyguladı. Ve bundan buldukları sonuç, ortalama IQ seviyesi puanı 120 ve varyans 121 idi. T puanının 2.407 olduğunu varsayalım. Bu test için popülasyon ortalaması nedir, bu t puanı değerini 2.407 olarak haklı çıkarır?
Çözüm:
T dağılımının hesaplanması için aşağıdaki verileri kullanın.

Burada tüm değerler t değeri ile birlikte verilmiştir; Bu sefer t değeri yerine popülasyon ortalamasını hesaplamamız gerekiyor.
Yine, mevcut verileri kullanacağız ve aşağıdaki formülde verilen değerleri girerek popülasyon ortalamalarını hesaplayacağız.
Örnek ortalama 120'dir, popülasyon ortalaması bilinmemektedir, örnek standart sapması varyansın karekökü olacaktır, bu 11 olacaktır ve örnek boyutu 50'dir.
Dolayısıyla, popülasyon ortalamasının (μ) hesaplanması aşağıdaki şekilde yapılabilir:
T dağılım formülünü kullanabiliriz.


T = (120 - μ) / (11 / √50) değeri
2,407 = (120 - μ) / (11 / √50)
-μ = -2.407 * (11 / √50) -120
Popülasyon Ortalaması (μ) -

μ = 116.26
Dolayısıyla, nüfus ortalamasının değeri 116,26 olacaktır.
Alaka ve Kullanım
T Dağılımı (ve ilişkili t skorları değerleri), hipotez testinde, kişinin boş hipotezi reddetmesi veya kabul etmesi gerekip gerekmediğini bulması gerektiğinde kullanılır.

Yukarıdaki grafikte, merkezi bölge kabul alanı, kuyruk bölgesi ise reddetme bölgesi olacaktır. 2 kuyruklu bir test olan bu grafikte mavi gölgeli ret bölgesi olacaktır. Kuyruk bölgesindeki alan, t-skorları veya z-skorları ile tanımlanabilir. Bir örnek alın; Soldaki resim, kuyruklarda yüzde beşlik bir alanı gösterecektir (bu, her iki tarafta da% 2,5'tir). Z-skoru 1.96 olmalıdır (z-tablosundaki değer alınarak), bu da ortalamadan veya ortalamadan 1.96 standart sapmayı temsil etmelidir. Z puanının değeri -1,96 değerinden düşükse veya z puanının değeri 1,96'dan büyükse boş hipotez reddedilebilir.
Genel olarak, bu dağılım, daha küçük bir örneklem büyüklüğüne (çoğunlukla 30'un altında) sahip olduğunda veya popülasyon varyansının veya popülasyon standart sapmasının ne olduğunu bilmediğinde daha önce açıklandığı gibi kullanılmalıdır. Pratik amaçlar için (yani gerçek dünyada), bu büyük ölçüde her zaman geçerli olacaktır. Sağlanan örneğin boyutu yeterince büyükse, 2 dağılım pratik olarak benzer olacaktır.








