Bileşik Tanımı
Bileşik faiz, faizin, yatırım / ilk anapara artı kazanılan faiz ve diğer yeniden yatırımlar üzerinden hesaplandığı, diğer bir deyişle kazanılan faizin mevduatın veya kredinin zaman dilimine bağlı olarak anapara tutarı kadar biriktirildiği, etkin faiz oranı olan faiz oranını hesaplama yöntemidir. bu aylık, üç aylık veya yıllık olabilir
Neyin birleştiğini ve nasıl çalıştığını bazı temel örneklerle anlamaya çalışalım.
Bileşik Oluşturmanın Gücü için İlk 4 Örnek
Örnek 1
Shane ve Mark, her ikisi de 1.00.000 $ yatırım yapmaya karar verdi, ancak Shane basit faize yatırım yapmaya karar verirken, Mark bileşik faize% 10 faizle on yıl boyunca yatırım yapıyor. On yıl sonra ne olacağını görelim.
Çözüm:
Öyleyse, Shane yatırımının hesaplanması -

Toplam Kazanç Tutarı = 200.000 $
Basit bir faizle, Shane 10 yıl sonra 2,00,000 $ alacak.
Mark yatırımının hesaplanması -

Toplam Kazanç Tutarı = 2,59,374 $
Bileşik faiz ile Mark'ın yatırım değerleri 2,59,374 dolara yükselecek.
Şimdi Shane, Mark gibi bileşik yöntemlerle yatırım yapmaya karar verdi ve ikisi de% 15 oranında 2.00.000 $ yatırım yaptı.
Shane yatırımının hesaplaması şöyle olacak:

Toplam Kazanç Tutarı = 8.09.111,55 $
Shane 10 yıl boyunca yatırımda kalır ve nihai tutarı% 15 oranında 8.09.111,55 $ olarak alır.
Mark yatırımının hesaplanması -

Toplam Kazanç Tutarı = 65,83,790,52 $
Bununla birlikte, Mark sabırlı uzun vadeli yatırımcılar ve 25 yıl boyunca yatırımda kalıyor ve yatırım değeri 65,83,790,52 dolara yükseliyor.
Yukarıdaki örnek, bileşik oluşturmanın gücünü göstermektedir. Yatırım ufku ne kadar uzunsa üssel büyüme o kadar büyük olur.
Örnek 2 (Haftalık)
Simon 7500 dolar birikim yapıyor ve 15 yıl sonra üniversiteye gidecek olan oğlunun üniversite fonu için ABD Tasarruf Tahvillerine yatırım yapmaya karar verdi. Simon'un hedefi 20.000 $ tasarruf etmek ve bir ABD tasarruf bonosu için yıllık yüzde oranı% 6. 15 yıl sonra Simon Money'nin Gelecekteki Değeri Nedir?
Çözüm:
Verilen,
- Anapara = 7500 $
- Oran =% 6 veya 0,06
- Zaman Periyodu = 15 yıl.
- Bir yılda kaç kez birleştirilir n = 52 Hafta
- Gelecek Değer =?
Yani, gelecekteki değerin hesaplanması -

Haftalık birleştirme formülü aşağıdaki gibidir.
F = P (1 + r / n) n * t- F = 7500 ABD doları (1 + 0,06 / 52) 52 * 15
- F = 7500 ABD doları (1 + 0,001153846) 780
- F = 18.437,45 ABD doları
Dolayısıyla, yukarıdaki hesaplamadan, Simon'un 20,00 $ tasarruf etme hedefinin yukarıdaki yöntemlerle elde edilmeyeceği açıktır, ancak buna daha yakın.
Sürekli Bileşik Yöntem
Şimdi yukarıdaki örneği Sürekli Bileşik Formülü ile deneyelim.
Yani, gelecekteki değerin hesaplanması -

- F = 7500e 0,06 * 15
- F = 7500e 0,9 ABD doları
- Gelecek Değer (F) = 18.447,02 $
Şimdi Continuous Compounding ile bile Simon'ın oğlunun üniversite fonu için 20.000 $ tasarruf etme hedefine ulaşılamayacak.
Aylık bileşik Formüle bakalım Simon'un% 6 APR ile 15 yılda 20.000 $ tasarruf etme hedefine ulaşmak için ne kadar para yatırması gerekiyordu?
Yani, gelecekteki değerin hesaplanması -
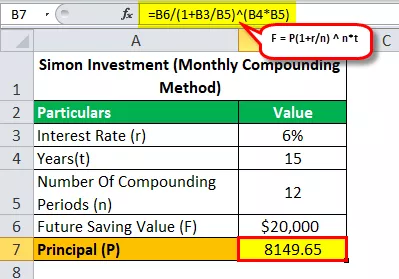
- 20.000 ABD Doları = P (1 + 0,06 / 12) 12 * 15
- P = 20.000 ABD doları / (1 + 0,06 / 12) 12 * 15
- Ana (P) = 8149.65
Dolayısıyla, yukarıdaki denklemi çözerek 8.149.65 $ 'lık bir cevap alacağız (Simon'un 15 yılda 20.000 $ tasarruf etme hedefine ulaşmak için yatırım yapması gereken tutar).
Örnek 3 (Efektif Yıllıklandırılmış Getiri)
Diyelim ki, XYZ limited bankası yaşlı vatandaşlara sabit mevduat için yıllık% 10 veriyor ve burada banka faizinin diğer tüm bankalar gibi üç ayda bir bileşik olduğunu varsayıyoruz. 5, 7 ve 10 yıllık efektif yıllık verimi hesaplayın.
Çözüm:
5 Yıllık Yıllık Verim:
- t = 5 yıl
- n = 4 (üç aylık bileşik)
- I = yıllık% 10
Yani A = (1 +% 10/100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- 5 Yılda I = 0.6386
Etkin Faiz = 0,6386 / 5
Etkili I = Yıllık% 12.772
7 Yıllık Yıllık Verim:
- t = 7 yıl
- n = 4 (üç aylık bileşik)
- I = yıllık% 10
Yani A = (1 +% 10/100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1.9965
- I = 7 Yılda 1.9965
- Etkili I = 0.9965 / 7
Etkili I = Yıllık% 14.236
10 Yıllık Yıllık Verim:
- t = 10 yıl
- n = 4 (üç aylık bileşik)
- I = yıllık% 10
Yani A = (1 +% 10/100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2.685
- I = 10 Yılda 1.685
- Etkili I = 1.685 / 10
Etkili I = Yıllık% 16.85
Örnek 4 - (Yıllık Gelirler: Gelecek Değer)
Her 3 ayda bir, yıllık% 4,8 oranında üç ayda bir bileşik olarak 1.000 $ yatırım yapılır. Annüity'nin 10 yılda değeri ne olacak?
Çözüm:
Öyleyse, Annüity'nin 10 yıl içinde ne kadar değerinde olacağını söylediğimizde, burada gelecekteki değeri bulmamız gerektiği anlamına gelir ve bu önemlidir, çünkü ne zaman yıllık gelirlerle ilgili bir örnek varsa, neyi bulmamız gerektiğini görmemiz gerekir.
Dolayısıyla, Gelecek Değerin formülü şu şekildedir:
Yıllık Gelir Getirisi = P ((1+ r) n - 1 / r)- P = Periyodik Ödeme
- r = Dönem başına oran
- n = dönem sayısı
Gelecek Değerin formülü şu şekildedir:
- Yani burada P = 1.000 $
- r = Yıllık% 4.8 veya 0.048
- r (üç aylık) = 0.048 / 4
- r (üç aylık) = 0,012
- n = 10 yıl
- n (Bileşimin uygulanma sayısı) = 10 × 4 = 40
Öyleyse, Yıllık Gelir FV'sinin hesaplanması -

Şimdi FV = 1000 $ (1 + 0.012) 40-1 / 0.012)
Dolayısıyla, yukarıdaki denklemi çözerek 50.955,30 $ FV elde edeceksiniz.
Öyleyse 10 yıl içinde Rant ne kadar olacak ve cevap 50.955.30 $
Ayrıca yukarıdaki örnekten 10 yılda ne kadar faiz kazandığını da öğrenebiliriz.
1000 $ 'ın 40 katı yatırım yapıldığında bu toplam yatırımdır (40 × 1000 $ = 40.000 $).
Yani Faiz = Gelecek Değer - Toplam yatırım
- Faiz = 50.955.30 - 40.000 $
- Faiz = 10.955.30 $
Öyleyse burada, Annuities'de yatırımcıların çok fazla faiz kazanabileceğini anlamak önemlidir. Yukarıdaki belirli örneklerde, 40.000 $ 'lık bir depozito karşılığında toplam 10.955.30 $ faiz verir.
Not: Ayrıntılı hesaplama için Yukarıda verilen Excel şablonunu indirebilirsiniz.








